The RIAA correction curve

The simplified RIAA amp look like this. R3 together with R1+R2 determines the DC-gain. In the following calculations R3 is only a constant.
The diagram above shows the response curves for both RIAA equalization, and the IEC modified version. The latter was not very popular, maybe because it represented a loss of bass (-3 dB ref RIAA at 20 Hz) or was it introduced too late?
RIAA time constants
The time constants that provide RIAA equalization are:
Low Frequency = 3180 us (50.05 Hz)
Mid Frequency = 318 us (500.5 Hz)
High Frequency = 75 us (2122 Hz)
The RIAA correction curve
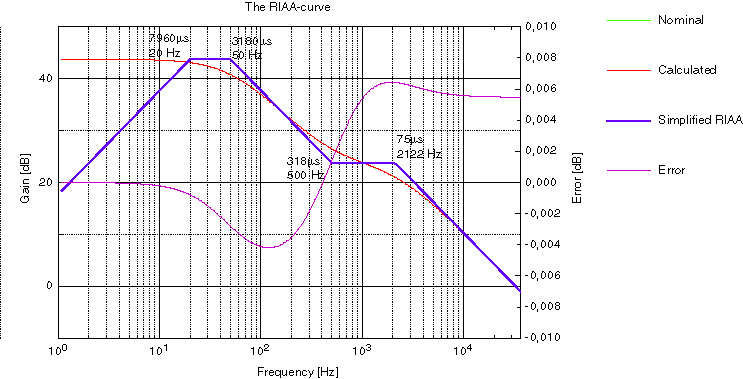
The diagram above shows the nominal and the calculated RIAA curve. The green curve is invisible because it lies almost exactly on top of the red one. If you look at the error curve, down below, you see why.
The diagram above shows the response curves for both RIAA equalization, and the IEC modified version. The latter was not very popular, maybe because it represented a loss of bass (-3 dB ref RIAA at 20 Hz) or was it introduced too late?
RIAA time constants
The time constants that provide RIAA equalization are:
Low Frequency = 3180 us (50.05 Hz)
Mid Frequency = 318 us (500.5 Hz)
High Frequency = 75 us (2122 Hz)
The RIAA-amp has a 'not very flat' frequency response. The reason for this is purely mechanical and exists to give both the cutter and the pickup a fair chance the do their job. The cutter is like a microphone or a loudspeaker. If you apply constant voltage to a loudspeaker you will notice that the movement (amplitude) of the cone is constant below the resonance frequency and above it, it is reversed proportional. If you double the frequency the movement will be half.
With this in mind, the grooves will get gigantic for bass tones and microscopical for the high ones. If you make the grooves very small they will be very sensitive for dust.
The first time constant at 50 Hz is to limit the cutters and the pickups movements in the low bass region below 50 Hz. Above 50 Hz the groove is cut with constant mechanical amplitude. The cutter has a resonance at 500 Hz. That is why the second time constant is at 500 Hz.
The 500 Hz knee suppresses the cutters resonance but you have still the dust problem. At 2122 Hz you will increase the treble and again cut the grooves with constant amplitude. This simple filter acts like a simple noise reduction.
If you remember the lessons from the schooldays you know that the output voltage is proportional to velocity. If the needle moves with a certain amplitude at 200 Hz and moves the same amplitude at 400 Hz you will get twice the output voltage. The signal increases with 6 dB/octave. This leaves us to design a amplifier with a filter that cut all frequencies with 6 dB/octave. But in the lowest region you don't have to cut.
It is this rather large amount of bass boost that accentuates the mechanical noise of a turntable, producing what is commonly known as "rumble". There is also the risk of low frequency feedback if the turntable is not capable of isolating the platter and tone-arm from the listening room environment. Timber floors and rigid suspension increase the risk of feedback.
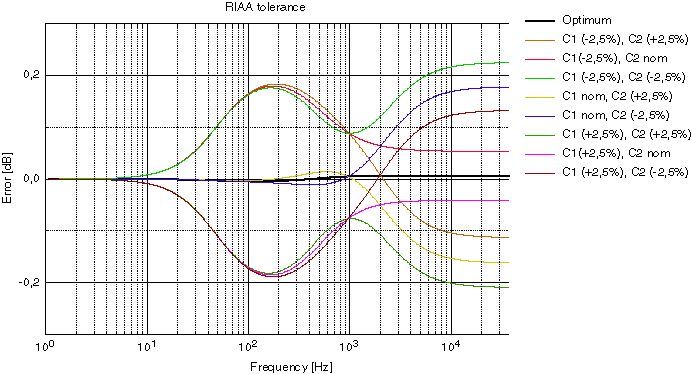
The RIAA error curve
The diagram above shows the nominal error (black) and the maximum of the calculated RIAA curve.
It's quite easy to acheive a very accurate RIAA correction curve. If you use 2,5% capacitors you should statisticly achieve a very accurate RIAA-curve. I think the maximun error will be 0,01-0,1 dB. I have derived the formulas and put them into a spreadsheet. Send me a mail if you want this Excel-file (version 8, Office 98). The nice diagrams above are made by the excellent program 'pro Fit' from QuantumSoft, www.quansoft.com.
The formulas are written with the freeware MathMagic from www.mathmagic.com

The simplified RIAA amp look like this. R3 together with R1+R2 determines the DC-gain. In the following calculations R3 is only a constant.
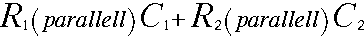
We are only interrested in the impedance of the feedback components.
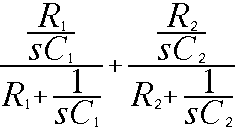
The parallell connection has this formula. "s" is a general frequency variable but can be replaced with the common jw (w=omega).
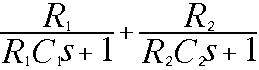
Simplify the expression.
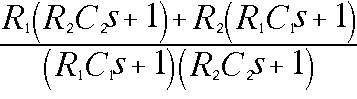
Interresting parts are everything in the numerator and the denominator. When everything gets zero in the numerator you have a "zero" which bends the curve up with 6 dB/octav. When some parts gets zero in the denominator you have a "pole" which bends the curve down with 6 dB/octav.
The result of this is that we want to find these solutions which gives us zeros. First we take the numerator.
![]()
![]()
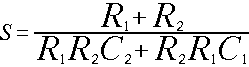
Above we have the solution for the "zero". The RIAA curve has only one zero which is at 500 Hz (s=318us)
![]()
The expression above is the denominator for the RIAA network. Now we shall look for any solutions that gives us zeros. The equation above is a common second degree equation. The solution is simple in this case.
This rather simple solution gives us two poles. Pole 1 is R1C1 and Pole 2 is R2C2, which is 50 Hz and 2122 Hz. Some parts in the expression are very small (you can omit them) but if you have a program at your help, it feels more comfortable to know that your answer is exact. I have made an Excel file for this. Mail me if you want it.
How do I get the values? You have to take a guess and then put them into the formula. Now it's nice to have a calculation program with good diagram capabilities.
Note
The RIAA network I have chosen to use works only with an inverting amplifier. If you use it with an non inverting amp, you will get an error becuase the gain will slowly get 1 instead of 0. When you make an MM-amp the error will get so big that you can hear it. A MC-amp has so much gain at 20 kHz that you won't notice this extra "zero"(bending of the frequency response upwards). This is true if the amp do the whole amplification. Do you use a pre amp the error will equally big as for MM-pickup.

